Implementing the Gradient Descent Algorithm¶
In this notebook, you'll be implementing the functions that build the gradient descent algorithm, namely:
sigmoid: The sigmoid activation function.output_formula: The formula for the prediction.error_formula: The formula for the error at a point.update_weights: The function that updates the parameters with one gradient descent step.
Your goal is to find the boundary on a small dataset that has two classes:
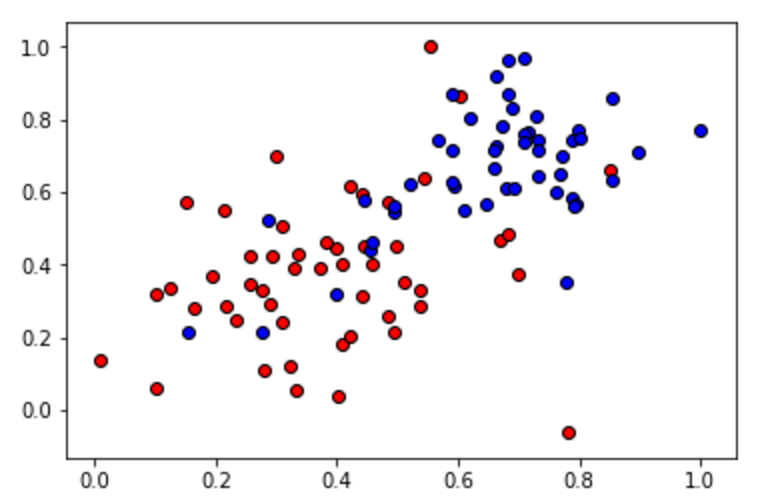
After you implement the gradient descent functions, be sure to run the train function. This will graph several of the lines that are drawn in successive gradient descent steps. It will also graph the error function, and you'll be able to see it decreasing as the number of epochs grows.
First, we'll start with some functions that will help us plot and visualize the data.
In [1]:
Copied!
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
#Some helper functions for plotting and drawing lines
def plot_points(X, y):
admitted = X[np.argwhere(y==1)]
rejected = X[np.argwhere(y==0)]
plt.scatter([s[0][0] for s in rejected], [s[0][1] for s in rejected], s = 25, color = 'blue', edgecolor = 'k')
plt.scatter([s[0][0] for s in admitted], [s[0][1] for s in admitted], s = 25, color = 'red', edgecolor = 'k')
def display(m, b, color='g--'):
plt.xlim(-0.05,1.05)
plt.ylim(-0.05,1.05)
x = np.arange(-10, 10, 0.1)
plt.plot(x, m*x+b, color)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
#Some helper functions for plotting and drawing lines
def plot_points(X, y):
admitted = X[np.argwhere(y==1)]
rejected = X[np.argwhere(y==0)]
plt.scatter([s[0][0] for s in rejected], [s[0][1] for s in rejected], s = 25, color = 'blue', edgecolor = 'k')
plt.scatter([s[0][0] for s in admitted], [s[0][1] for s in admitted], s = 25, color = 'red', edgecolor = 'k')
def display(m, b, color='g--'):
plt.xlim(-0.05,1.05)
plt.ylim(-0.05,1.05)
x = np.arange(-10, 10, 0.1)
plt.plot(x, m*x+b, color)
Reading and plotting the data¶
In [2]:
Copied!
data = pd.read_csv('data.csv', header=None)
X = np.array(data[[0,1]])
y = np.array(data[2])
plot_points(X,y)
plt.show()
data = pd.read_csv('data.csv', header=None)
X = np.array(data[[0,1]])
y = np.array(data[2])
plot_points(X,y)
plt.show()
TODO: Implementing the basic functions¶
Here is your turn to shine. Implement the following formulas, as explained in the text.
- Sigmoid activation function
$$\sigma(x) = \frac{1}{1+e^{-x}}$$
- Output (prediction) formula
$$\hat{y} = \sigma(w_1 x_1 + w_2 x_2 + b)$$
- Error function
$$Error(y, \hat{y}) = - y \log(\hat{y}) - (1-y) \log(1-\hat{y})$$
- The function that updates the weights
$$ w_i \longrightarrow w_i + \alpha (y - \hat{y}) x_i$$
$$ b \longrightarrow b + \alpha (y - \hat{y})$$
In [3]:
Copied!
# Activation (sigmoid) function
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# Output (prediction) formula
def output_formula(features, weights, bias):
return sigmoid(np.dot(features, weights) + bias)
# Error (log-loss) formula
def error_formula(y, output):
return - y*np.log(output) - (1 - y) * np.log(1-output)
# Gradient descent step
def update_weights(x, y, weights, bias, learnrate):
output = output_formula(x, weights, bias)
d_error = y - output
weights += learnrate * d_error * x
bias += learnrate * d_error
return weights, bias
# Activation (sigmoid) function
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# Output (prediction) formula
def output_formula(features, weights, bias):
return sigmoid(np.dot(features, weights) + bias)
# Error (log-loss) formula
def error_formula(y, output):
return - y*np.log(output) - (1 - y) * np.log(1-output)
# Gradient descent step
def update_weights(x, y, weights, bias, learnrate):
output = output_formula(x, weights, bias)
d_error = y - output
weights += learnrate * d_error * x
bias += learnrate * d_error
return weights, bias
Training function¶
This function will help us iterate the gradient descent algorithm through all the data, for a number of epochs. It will also plot the data, and some of the boundary lines obtained as we run the algorithm.
In [4]:
Copied!
np.random.seed(44)
epochs = 100
learnrate = 0.01
def train(features, targets, epochs, learnrate, graph_lines=False):
errors = []
n_records, n_features = features.shape
last_loss = None
weights = np.random.normal(scale=1 / n_features**.5, size=n_features)
bias = 0
for e in range(epochs):
del_w = np.zeros(weights.shape)
for x, y in zip(features, targets):
output = output_formula(x, weights, bias)
error = error_formula(y, output)
weights, bias = update_weights(x, y, weights, bias, learnrate)
# Printing out the log-loss error on the training set
out = output_formula(features, weights, bias)
loss = np.mean(error_formula(targets, out))
errors.append(loss)
if e % (epochs / 10) == 0:
print("\n========== Epoch", e,"==========")
if last_loss and last_loss < loss:
print("Train loss: ", loss, " WARNING - Loss Increasing")
else:
print("Train loss: ", loss)
last_loss = loss
predictions = out > 0.5
accuracy = np.mean(predictions == targets)
print("Accuracy: ", accuracy)
if graph_lines and e % (epochs / 100) == 0:
display(-weights[0]/weights[1], -bias/weights[1])
# Plotting the solution boundary
plt.title("Solution boundary")
display(-weights[0]/weights[1], -bias/weights[1], 'black')
# Plotting the data
plot_points(features, targets)
plt.show()
# Plotting the error
plt.title("Error Plot")
plt.xlabel('Number of epochs')
plt.ylabel('Error')
plt.plot(errors)
plt.show()
np.random.seed(44)
epochs = 100
learnrate = 0.01
def train(features, targets, epochs, learnrate, graph_lines=False):
errors = []
n_records, n_features = features.shape
last_loss = None
weights = np.random.normal(scale=1 / n_features**.5, size=n_features)
bias = 0
for e in range(epochs):
del_w = np.zeros(weights.shape)
for x, y in zip(features, targets):
output = output_formula(x, weights, bias)
error = error_formula(y, output)
weights, bias = update_weights(x, y, weights, bias, learnrate)
# Printing out the log-loss error on the training set
out = output_formula(features, weights, bias)
loss = np.mean(error_formula(targets, out))
errors.append(loss)
if e % (epochs / 10) == 0:
print("\n========== Epoch", e,"==========")
if last_loss and last_loss < loss:
print("Train loss: ", loss, " WARNING - Loss Increasing")
else:
print("Train loss: ", loss)
last_loss = loss
predictions = out > 0.5
accuracy = np.mean(predictions == targets)
print("Accuracy: ", accuracy)
if graph_lines and e % (epochs / 100) == 0:
display(-weights[0]/weights[1], -bias/weights[1])
# Plotting the solution boundary
plt.title("Solution boundary")
display(-weights[0]/weights[1], -bias/weights[1], 'black')
# Plotting the data
plot_points(features, targets)
plt.show()
# Plotting the error
plt.title("Error Plot")
plt.xlabel('Number of epochs')
plt.ylabel('Error')
plt.plot(errors)
plt.show()
Time to train the algorithm!¶
When we run the function, we'll obtain the following:
- 10 updates with the current training loss and accuracy
- A plot of the data and some of the boundary lines obtained. The final one is in black. Notice how the lines get closer and closer to the best fit, as we go through more epochs.
- A plot of the error function. Notice how it decreases as we go through more epochs.
In [5]:
Copied!
train(X, y, epochs, learnrate, True)
train(X, y, epochs, learnrate, True)
========== Epoch 0 ========== Train loss: 0.713584519538 Accuracy: 0.4 ========== Epoch 10 ========== Train loss: 0.622583521045 Accuracy: 0.59 ========== Epoch 20 ========== Train loss: 0.554874408367 Accuracy: 0.74 ========== Epoch 30 ========== Train loss: 0.501606141872 Accuracy: 0.84 ========== Epoch 40 ========== Train loss: 0.459333464186 Accuracy: 0.86 ========== Epoch 50 ========== Train loss: 0.425255434335 Accuracy: 0.93 ========== Epoch 60 ========== Train loss: 0.397346157167 Accuracy: 0.93 ========== Epoch 70 ========== Train loss: 0.374146976524 Accuracy: 0.93 ========== Epoch 80 ========== Train loss: 0.354599733682 Accuracy: 0.94 ========== Epoch 90 ========== Train loss: 0.337927365888 Accuracy: 0.94
In [ ]:
Copied!